Veja também:

• Os últimos números da pandemia em Portugal e no mundo
• Todas as notícias sobre a pandemia de Covid-19
• Guias e explicadores: as suas dúvidas esclarecidas
• Boletins Covid-19: gráficos, balanços e outros números

Os testes serológicos podem vir a mudar as regras do jogo no que toca à gestão da pandemia de Covid-19. Quem o defende é o matemático britânico Kit Yates, em entrevista à Renascença.

Crítico do Governo britânico durante a primeira vaga, pelo que considera ter sido a lentidão no anúncio do confinamento do país, o matemático e biólogo pede uma resposta equilibrada à atual segunda vaga da pandemia na Europa, espelhada em novos picos de infeções por Covid-19 em vários países, com o Reino Unido à cabeça.

Antes desta pandemia, já Kit Yates explicava a importância do R0 para calcular o ritmo de propagação de uma doença e antecipar o comportamento de determinado surto.

Em "As Fórmulas da Vida e da Morte", editado em Portugal pela Desassossego, o matemático vai ainda mais longe, mostrando como os números estão em tudo o que somos e fazemos: na forma como comunicamos, nas viagens, no trabalho ou nos momentos de lazer. A forma como utilizamos a matemática pode determinar uma sentença em tribunal, uma decisão hospitalar ou se conseguimos o primeiro milhão, como nos conta o autor através de casos reais.

No livro, Kit Yates dá dicas de como usar a matemática no dia a dia, em nosso benefício. Nesta entrevista à Renascença, mergulha ainda na polémica sobre os dados estatísticos que hoje invadem os media, as redes sociais e os espaços de discussão, cujas fontes nem sempre são fidedignas.

As estatísticas podem mentir?

Jornalistas e políticos são frequentemente acusados de mentir com estatísticas. Na era das notícias falsas, é difícil saber em quem confiar. Acredite-se ou não, a maioria dos principais meios de comunicação baseia a maior parte das histórias em fatos. Veracidade e exatidão estão no top (se não no topo) da lista de quase todos os códigos de ética e integridade jornalística. No entanto, muitas organizações de media diferem no relato dos fatos, na perspetiva com que apresentam a história. O partidarismo é fácil de detectar nas declarações das pessoas. Já os números, por outro lado, são fáceis de trabalhar sub-repticiamente.

As estatísticas podem ser escolhidas a dedo para apresentar um ângulo específico de uma história. Outras figuras são totalmente ignoradas e histórias deturpadas, criadas puramente por omissão. Às vezes, são os próprios estudos que não são confiáveis. Amostras pequenas, não representativas ou tendenciosas, em conjunto com perguntas direcionadas e relatórios seletivos, podem gerar estatísticas não confiáveis.

Mais subtis ainda são as estatísticas utilizadas fora de contexto, de modo que não temos como julgar se, por exemplo, um aumento de 300% nos casos de uma doença representa um aumento de 1 paciente para 4 ou de 500 mil pacientes para 2 milhões.

A falha está na leitura dos números.

O contexto é importante. Essas diferentes interpretações dos números não são mentiras - cada uma é um pequeno pedaço da história verdadeira sobre a qual alguém iluminou o que quis destacar – mas não é toda a verdade. É preciso reunir a verdadeira história por trás da hipérbole.

Era possível antecipar o alerta global para a Covid-19, tendo em conta as fórmulas matemáticas disponíveis atualmente?

Em termos muito gerais, sim. A matemática e as ciências, de um modo geral, têm sido usadas para prever a probabilidade de tais eventos.

Em “As Fórmulas da Vida e da Morte”, explico que “as doenças zoonóticas, como as estripes originais do HIV, que saltam entre espécies, são uma das maiores ameaças potenciais à saúde pública.” Ao que parece, é exatamente o que aconteceu com o SARS-Cov-2. De um modo geral, dadas todas as advertências dos organismos de saúde pública, como a OMS, devíamos estar mais bem preparados para uma pandemia a esta escala. No entanto, em termos de previsão de uma data, local ou tipo de doença específico, isso ultrapassa os domínios da ciência e da matemática modernas.

"Devíamos estar mais bem preparados para uma pandemia a esta escala"

Perante tantos falsos positivos, do ponto de vista matemático, podemos confiar no resultado dos testes à Covid-19?

Se os testes derem até mesmo uma pequena taxa de falsos positivos, e estivermos a testar grandes faixas da população que estão praticamente livres de doenças, a maioria dos testes que dão positivo podem ser falsos positivos.

O problema dos falsos positivos ultrapassarem os verdadeiros positivos ocorre em qualquer situação em que a prevalência de determinada doença na população testada é baixa e o teste fornece uma proporção significativa de falsos positivos. Como revelo em “As fórmulas da Vida e da Morte”, é uma situação comum em programas de triagem. No rastreamento do cancro da mama, por exemplo, por cada verdadeiro positivo podem aparecer três falsos positivos, o que conduz a situações de ansiedade significativa e potencia procedimentos desnecessários.

Porém, vale a pena lembrar que serão sobretudo testadas pessoas com sintomas, o que implica que a probabilidade de que tenham Covid será significativamente maior do que na população em geral. Nestes casos, o impato dos falsos positivos pode ser significativamente menor.

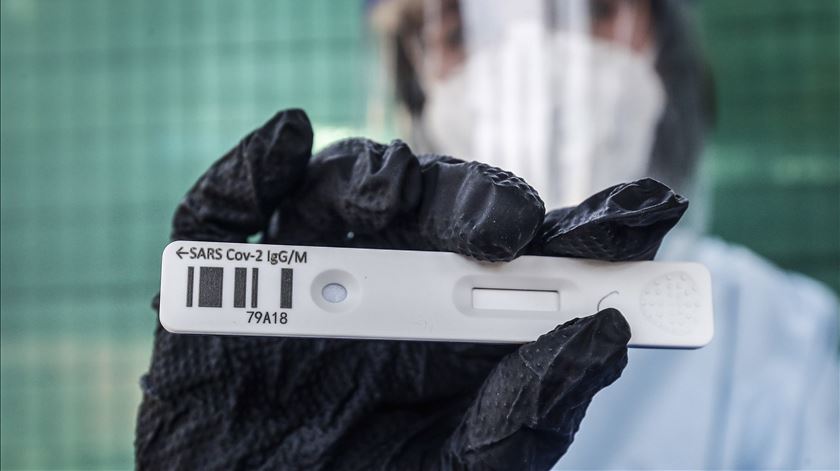
Os testes serológicos podem enviar as pessoas para o trabalho cedo demais?

Os testes de anticorpos podem mudar as regras do jogo, ao manter o público protegido contra infeções enquanto reinicia a economia. Dar “passaportes de imunidade” aos que tiveram resultado positivo para a doença permitiria que milhares de pessoas voltassem ao trabalho em segurança.

No entanto, a nova ideia é polémica. O mais importante na mente de muitas pessoas são as implicações éticas. Pessoas em circunstâncias económicas difíceis podem, perversamente, ser incentivadas a contrair a doença para que possam retornar ao trabalho. Para outros, as questões de privacidade relacionadas com o armazenamento centralizado de dados médicos são um obstáculo. A Organização Mundial da Saúde (OMS) também lançou dúvidas sobre até que ponto as pessoas que recuperaram de Covid-19 estarão protegidas de futuros contágios.

Também aqui, podem existir falsos positivos.

Tal como acontece com os testes de despistagem, ainda que a taxa seja pequena, se existirem falsos positivos, é possível que os resultados positivos sejam falsos positivos. Um grande número de pessoas com resultados falsos positivos, quando devolvidas ao mercado de trabalho, correm o risco de se infetarem e de disseminarem a doença para outras pessoas, sem saberem, o que desencadeia uma maior disseminação da epidemia.

Em maio criticou o Governo britânico pela demora em avançar com o confinamento, diz que bastava uma semana antes e teria sido possível salvar milhares de vidas. Se a segunda vaga se confirmar, os governos devem aprovar novo confinamento até que haja uma vacina?

À medida que as coisas começam a sair do controlo novamente, como vimos em grande parte da Europa, os governos enfrentarão decisões difíceis. Outro bloqueio irá permitir controlar a doença rapidamente, mas há um equilíbrio a ser alcançado. Existem medidas que não chegam a um bloqueio total que podem controlar a doença, permitindo que as escolas continuem abertas e as pessoas a trabalhar. Mas é um ato de equilíbrio. Teremos que sacrificar algumas das coisas que gostamos de fazer para permitir que outras coisas continuem inalteradas. Certamente, não podemos simplesmente continuar como se nada estivesse a acontecer, enquanto os casos aumentam.

"Um grande número de pessoas com resultados falsos positivos, quando devolvidas ao mercado de trabalho, correm o risco de se infetarem e de disseminarem a doença"

A matemática também terá um papel na vacinação, desde os ensaios clínicos até à distribuição?

Absolutamente! As estatísticas já estão a ser aplicadas, para determinar quantas pessoas são necessárias para os testes, de modo a garantir que as vacinas são seguras. As estatísticas são uma parte extremamente importante de todos os ensaios clínicos modernos de medicamentos. Certamente, a matemática também irá desempenhar um grande papel na logística de distribuição da vacina. É ainda justo dizer que a matemática determinará a proporção de pessoas que vão precisar da vacina para induzir a imunidade coletiva, que acabará por nos livrar da própria vacina.

Atreve-se a calcular quantas pessoas podem morrer na atual pandemia?

Vai depender do nosso comportamento. Se formos sensatos e mantivermos distância das pessoas, se lavarmos as mãos e usarmos máscaras em situações em que não podemos manter a distância, será possível controlar a propagação da doença. Mas é um esforço coletivo. Temos que pensar uns nos outros, em usar máscaras não apenas para nos proteger, mas para proteger os nossos vizinhos. Se não agirmos com rapidez suficiente para controlar os surtos, as coisas podem rapidamente sair do nosso controle mais uma vez.

Uma vez que muito depende do nosso comportamento, não faz sentido tentar chegar a um número de pessoas que podem eventualmente sucumbir a esta doença.

É possível prever o retorno à normalidade?

Isso depende muito do momento da vacinação, porque uma vacinação eficaz é a única saída para esta pandemia. O vírus está em todo o mundo e as intervenções não farmacêuticas não serão suficientes. Se ouvir Donald Trump, pode acreditar que a vacina estará pronta para distribuição em apenas alguns meses. Se ouvir os especialistas, eles preveem que será em meados de 2021, no mínimo.

Neste livro descreve como os números influenciam as nossas vidas, para o melhor e para o pior. Eles podem até levar à morte?

Sim, em algumas circunstâncias, os erros matemáticos podem realmente ser uma questão de vida ou morte. Uma das histórias que conto é a de Mary Williams, uma pensionista de 85 anos, para quem representou exatamente isso. No dia 2 de junho de 2007, a enfermeira comunitária, Joanne Evans, visitou a Sra. Williams, como um favor a uma colega. Evans foi acusada de aplicar a injeção de insulina na paciente diabética naquele dia.

"Há medidas que não chegam a um bloqueio total e que podem controlar a doença, permitindo que as escolas continuem abertas e as pessoas a trabalhar. Mas é um ato de equilíbrio"

Ela encheu a caneta de injeção de insulina com as 36 ‘unidades’ de insulina necessárias, mas, ao tentar injetá-la, a caneta emperrou. Tentou com outras duas canetas que trouxera, mas cada uma falhou. Preocupada com o que aconteceria à Sra. Williams se não recebesse a insulina, a enfermeira voltou ao carro para procurar uma seringa comum. Embora as canetas fossem marcadas simplesmente em 'unidades' de insulina e a seringa em mililitros, Evans sabia que cada 'unidade' correspondia a 0,01 mililitros. Encheu a seringa de um mililitro e injetou no braço da Sra. Williams, um processo que repetiu mais três vezes para completar a dosagem, sem se questionar por que administrava várias injeções quando uma única dose tinha sido suficiente para os outros pacientes.

Com o trabalho finalmente concluído, deixou a Sra. Williams e seguiu para outros pacientes. Só mais tarde naquele dia percebeu o terrível erro: em vez de injetar 0,36 mililitros de insulina, tinha dado 3,6 mililitros à Sra. Williams - dez vezes mais. Imediatamente chamou um médico, mas a Sra. Williams já tinha sofrido um ataque cardíaco fatal, induzido pela insulina.

Mas também há exemplos de fórmulas com um final feliz ...

De um modo geral, a matemática tem um lado bom e mau. A matemática são os falsos alarmes que disparam na nossa cabeça e a falsa confiança que nos ajuda a dormir à noite; as histórias e os memes que chegam até nós e se espalham nas redes sociais.

A matemática são as lacunas na lei e a agulha que as fecha; a tecnologia que salva vidas e os erros que as colocam em risco; o surto de uma doença mortal e a melhor maneira de controlá-la. É a melhor esperança que temos de responder às questões fundamentais sobre os enigmas do cosmos e os mistérios da nossa própria espécie. Ela conduz-nos por uma miríade de caminhos nas nossas vidas e fica à espreita, atrás do véu, para nos olhar nos olhos no momento do último suspiro.

Muitas pessoas têm dificuldade em ver o mundo da mesma perspetiva, são avessas a números e desistiram desde cedo da matemática.

Acredito genuinamente que a matemática é para todos e que todos nós podemos apreciar a beleza da matemática no centro dos fenómenos complicados que vivenciamos diariamente. Como especialista em matemática aplicada, vejo a matemática, antes de mais, como uma ferramenta prática para dar sentido ao nosso mundo complexo. Os modelos matemáticos podem colocar-nos em vantagem nas situações do quotidiano e, para isso, não é necessário envolver centenas de equações aborrecidas ou linhas de código de computador.

A matemática, na sua forma mais fundamental, são padrões. Cada vez que cada um de nós olha para o mundo, construímos o nosso próprio modelo dos padrões que observamos. Se identificarmos um motivo nos galhos fractais de uma árvore ou na simetria de múltiplas dobras de um floco de neve, estamos a ver matemática. Quando bate o pé ao ritmo de uma peça musical ou quando a voz reverbera e ressoa ao cantar no chuveiro, está a ouvir matemática. Se rematar para o fundo da baliza ou apanhar uma bola de críquete em trajetória parabólica, está a fazer matemática.

"Acredito genuinamente que a matemática é para todos e que todos nós podemos apreciar a beleza da matemática no centro dos fenómenos complicados que vivenciamos diariamente"

E como nos pode ajudar a matemática no dia a dia? Pode deixar algumas dicas?

Uma das minhas ferramentas matemáticas favoritas é a optimal stopping (distancia ideal de travagem). Imagine, por exemplo, que procura um restaurante para ir jantar fora com o seu parceiro. Quer qualidade e não vai ficar com a primeira opção que aparecer. Confia que tem capacidade para comparar restaurantes e descobre que terá tempo para avaliar até 10 opções antes que o seu parceiro se canse de deambular. Como não quer parecer indeciso, decide que não voltará a um restaurante depois de rejeitá-lo.

A melhor estratégia é olhar e rejeitar alguns restaurantes de imediato, para ter uma ideia das opções disponíveis. Podia escolher o primeiro restaurante que visitar, mas como não tem absolutamente nenhuma informação, há apenas 1 possibilidade em 10 de escolher o melhor aleatoriamente. Portanto, o melhor será julgar uma série de restaurantes primeiro.

Quando decide cedo demais está a adivinhar às cegas, nesta situação a probabilidade é baixa. Da mesma forma, quando espera muito tempo, é provável que já tenha perdido a melhor opção. A matemática por trás do problema é complicada, mas parece que deve julgar e rejeitar aproximadamente os primeiros 37% restaurantes (arredondados para 3 se houver apenas 10) antes de aceitar o próximo, que é melhor do que todos os anteriores.

Esta regra pode ser aplicada em várias situações?

Não funciona apenas para restaurantes. Na verdade, o problema chamou a atenção dos matemáticos pela primeira vez como o "problema da contratação". Se tiver que entrevistar um determinado número de candidatos para um emprego, um após o outro, e no final de cada entrevista, tem que dizer ao candidato se ele conseguiu o emprego ou não, use a regra dos 37%. Entreviste 37% dos candidatos e use-os como referência. Fique com o primeiro entrevistado depois daquele que é melhor do que todos os outros que viu até agora e rejeite o resto.

Quando chego à caixa do meu supermercado local, passo pelos primeiros 37% (4 de 11), observando passivamente o tamanho e entro na primeira fila, que é mais curta do que todas as outras. Se estou a competir, com um grupo de amigos, pelo último comboio lotado depois de uma noite fora e queremos encontrar a carruagem com mais lugares disponíveis para ficarmos todos juntos, usamos a regra dos 37%. Passamos pelas três primeiras carruagens, num comboio de oito, lembrando-nos de como estão vazios, e escolhemos a primeira carruagem que tem mais assentos livres do que qualquer uma das três primeiras.